|
2. Kepler-Gesetz:
Die Flächengeschwindigkeit der
Planeten ist konstant.
|
A Was ist die Flächengeschwindigkeit?
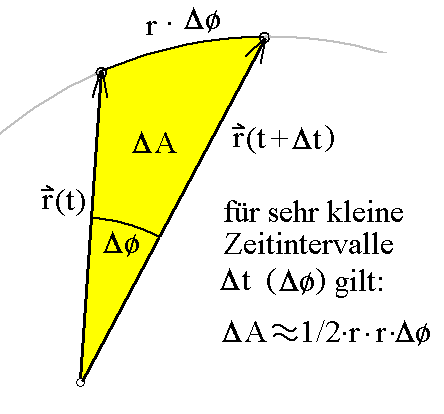 |
In einem Zeitabschnitt Δt überstreicht der Fahrstrahl (der
Radiusvektor r) von der Sonne bis zum Planeten eine Fläche
ΔA. Unter Flächengeschwindigkeit versteht man das Verhältnis
ΔA/Δt, also so etwas wie "überstrichene Fläche pro Zeiteinheit".
Wenn man mit Hilfe der Bogenlänge b = r·Δφ für sehr kleine
Zeitintervalle Δt bzw. sehr kleine Winkeländerungen Δφ die vom
Fahrstrahl überstrichene Fläche ansetzt, erhält man ungefähr ΔA
= 1/2·r·r·Δφ (1/2 x Radius x
Bogenlänge). Damit ergibt sich
ΔA/Δt = 1/2 · r2 · ω mit der Winkelgeschwindigkeit
ω = Δφ/Δt. Entsprechendes gilt auch im Limes Δt => 0.
|
Diese Flächengeschwindigkeit ist also konstant.
Die Flächengeschwindigkeit hängt mit dem Betrag des so genannten
Drehimpulses des umlaufenden Planeten bzgl. der Sonne zusammen. Aus der
Definition des Drehimpulses, auf die hier nicht näher eingegangen werden
soll (L = r x p), ergibt sich: Dieser Drehimpuls
steht senkrecht auf dem Fahrstrahl (r) und dem
Geschwindigkeitsvektor (also auch dem Impulsvektor p). L
steht also senkrecht auf der Bahnebene, sagen wir in z-Richtung. Für
seinen Betrag gilt: /L/ = m r2ω = 2·m·ΔA/Δt mit der
Planetenmasse m, dem momentanen Bahnradius r und der Winkelgeschwindigkeit
ω.
B Worin besteht die Aussage des Gesetzes?
1. Der Drehimpuls L ist konstant. Es gibt kein Drehmoment M,
das den Drehimpuls L verändert, weder der Richtung nach (d.h. die
Lage der Bahnebene senkrecht zu L bleibt unverändert), noch dem
Betrag nach (d.h. die Winkelgeschwindigkeit ω kann nur in einer bestimmten
Weise mit dem Radius r zusammenhängen.)
2. In der Nähe des Perihels (sonnennächster Punkt der Bahn) muss die
Winkelgeschwindigkeit ω des umlaufenden Planeten größer sein als in der
Nähe des Aphels (sonnenfernster Punkt der Bahn): Der Winter ist etwas
kürzer als der Sommer. (Dass es im Winter in der Regel kälter ist als im
Sommer liegt nicht daran, sondern an unterschiedlichen Einfallswinkeln der
Sonnenstrahlung.)
C Welche physikalischen Folgerungen ergeben sich aus dem 2.
Kepler-Gesetz:
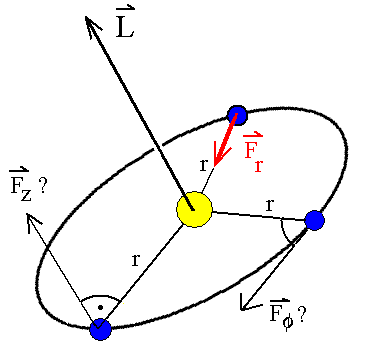
| 1. Die wirkende Kraft ist eine reine Zentralkraft. Sie
hat keine Komponenten in φ oder in z-Richtung. Denn diese würden
Drehmomente M erzeugen (Hebelarme jeweils r), die den
Drehimpulsvektor ändern, wie anschaulich einsichtig ist (Abb.).
Die Zentralkraft bewirkt kein Drehmoment (verschwindender
Hebelarm).
2. Die wirkende Kraft kann nicht dafür sorgen, dass sich
die Planeten von Umlauf zu Umlauf immer schneller oder immer
langsamer um die Sonne bewegen. Die Umlaufszeit bleibt konstant
und damit auch die Energie des Planeten: Eine Zentralkraft ist
ja auch eine konservative Kraft, für die der
Energieerhaltungssatz gilt.
Hinweis: Eine reine Zentralkraft ist auch aus
Symmetriegründen naheliegend. Ähnlich symmetrisch wäre nur noch
eine azimutal wirkende Kraft (mit geschlossenen Feldlinien) um
die Sonne herum. Während uns eine solche Kraft ungewöhnlich
erscheinen würde (wir haben ja längst von der Gravitationskraft
gehört), glaubte noch Kepler in Unkenntnis von Newtons Mechanik,
dass die Planeten gerade durch solche azimutalen Kräfte um die
Sonne "herumgewirbelt" werden.
|
 |
D Zum Zusammenhang zwischen Drehimpuls und Flächengeschwindigkeit
Üblicherweise ist der Begriff Drehimpuls in der Schule unbekannt zu dem
Zeitpunkt, wenn die Kepler-Gesetze behandelt werden. Ein Teil dieses
Textes wird also an der Stelle unverständlich bleiben. Nach vielen
Lehrplänen soll jedoch die Drehung starrer Körper behandelt werden. Von
dort ist dann die Definition des Drehimpulses bekannt und der dem 2. NG
entsprechende Zusammenhang zwischen Änderungsgeschwindigkeit des
Drehimpulses dL/dt und dem Drehmoment M. Es könnte sinnvoll
sein, dort noch einmal die Kepler-Bewegung aufzugreifen. Obwohl die
entsprechenden Gesetze für die Rotation starrer Körper behandelt werden,
lassen sie sich auf den Umlauf von Punktmassen übertragen. Also
(1) L = Θ ω wobei das Trägheitsmoment für eine
Punktmasse m im Abstand r vom Bezugspunkt Θ = mr2 .
Das begründet L = mr2 ω . Daraus folgt dA/dt
= m/2·L = konst.
(2) Wenn also die Flächengeschwindigkeit dA/dt konstant ist, muss
der Drehimpuls konstant bleiben. Geändert werden könnte er durch ein
Drehmoment M : dL/dt = M (analog zum 2.
Newton-Gesetz: dp/dt = F )
Zu einer radialen Komponente der Kraft würde verschwindender Hebelarm
gehören. Sie kann also keinen Beitrag zum Drehmoment liefern, wohl aber
eine z-Komponente (r·Fz ) und eine azimutale Komponente
(r·Ff ) mit den
jeweiligen Hebelarmen r. Wenn der Drehimpuls konstant ist, müssen also Fz
und Ff verschwinden. Der Flächensatz
ist allein mit einer Radialkraft verträglich!
In der Literatur findet man auch formale Nachweise für das Verschwinden
einer azimutalen und axialen Komponente von Beschleunigung und Kraft in
Zylinderkoordinaten. Dort erhält man einen Ausdruck für die azimutale
Beschleunigung bzw. Kraft, der gleich der Ableitung der konstanten
Flächengeschwindigkeit, also 0, ist.

