Startseite FORPHYS Physik für Schülerinnen und Schüler Didaktogene Lernschwierig- keiten im Physik-UR An- schauliche Mechanik   Elektrischer Stromkreis   Schüler- versuche Physik Lernen mit dem Computer  Meta- Physika- lisches  Begriff- liches Experi- ment des Monats Im- pres- sum Kommen- tare und Wünsche © Horst Hübel Würzburg 2005 - 2014

Wurf

I Nach Erinnerung an Wurfbewegungen in der Umwelt der Schüler steht zunächst der physikalische Aspekt im Zentrum, dass beim Wurf zwei überlagerte Bewegungen gleichzeitig ablaufen, die für sich mit den bekannten Methoden untersucht werden können: eine gleichförmige Bewegung mit konstanter Geschwindigkeit vx0 in horizontaler Richtung und ein Freier Fall in vertikaler Richtung. Hilfsmittel zur Erarbeitung dieser Tatsachen können sein:

• der Versuch mit dem Wurfapparat, der zeigt, dass die Vertikalbewegung von Freiem Fall und horizontalem Wurf identisch sind (wenigstens in den Fallzeiten),
• der Affenschuss-Versuch von Prof. Scheer (Uni Würzburg), der dasselbe viel eindrucksvoller und eigentlich für beliebige Zeitpunkte der Bewegung zeigt,
• Videoaufnahmen von Würfen, insbesondere von einem Vergleich zwischen Freien Fall und horizontalem Wurf
• Simulationen zu diesen Versuchen

Videoaufnahmen können in verschiedener Weise ausgewertet werden:

• indem mit einem geeigneten Standard-Graphik-Programm Einzelbilder aus dem Video ausgeschnitten und überlagert werden,
• indem in Einzelbildschaltung ein Bild nach dem anderen auf den Bildschirm gebracht wird. Die jeweiligen Positionen des geworfenen Körpers werden auf einer auf dem Bildschirm aufliegenden Folie markiert und anschließend auf dem Tageslichtprojektor ausgewertet.
• indem das Video mit Hilfe eines Videoauswertungsprogramms (z.B. DIVA oder GALILEO (Klett-Verlag)) auswertet wird.

Beispiel: Überlagerte Einzelbilder eines Videos zum horizontalen Wurf. Hier wird eine Negativ-Darstellung gewählt, weil die günstigeren Helligkeitsverhältnisse es den Schülern erleichtern, in Papierkopien davon horizontale und vertikale Visierlinien einzutragen. (Die Skalen im Hintergrund sind weniger brauchbar).

Als griffige Merkregel, um dies zu erleichtern, hat sich bewährt:

Trotz der etwas merkwürdigen Formulierung enthält der Satz eine klare Arbeitsanweisung:  Wenn Du die Wurfweite berechnen willst, brauchst Du die Fallzeit! Auch für andere Fragestellungen hat sich der Satz als Ausgangspunkt für elementare Überlegungen bewährt. Einsetzen in fertige "Formeln" ist m.E. in diesem Zusammenhang sinnlos.

II Der nächste Schritt einer "Theoretisierung" besteht darin, von unabhängigen Bewegungen in horizontaler und vertikaler Richtung zu Vektoren zu kommen. Dabei sollen nicht Spalten- (oder Zeilen-)Vektoren im Mittelpunkt stehen, sondern Vektoren in koordinatenfreier Darstellung, weil an ihnen die physikalischen Sachverhalte deutlicher erscheinen als in Koordinatendarstellungen.

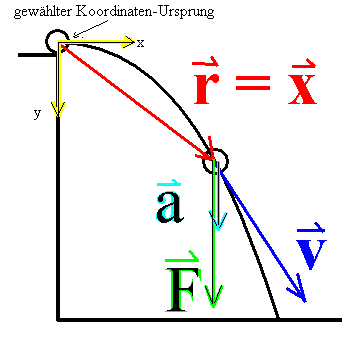Aus den Überlegungen des Abschnitts I sind die Richtungen von Vektoren klar: der Geschwindigkeitsvektor v ist definitionsgemäß in jedem Punkt der Bahn parallel zur Bewegungsrichtung, also längs der Tangente an die Bahnkurve gerichtet der Beschleunigungsvektor a ist (nach dem anfänglichen Beschleunigungsvorgang) ausschließlich vertikal nach unten gerichtet die einzig wirkende Kraft F, die Gewichtskraft ist ebenfalls ausschließlich vertikal und damit gleichgerichtet zur Beschleunigung a orientiert. Daneben kann noch ein Ortsvektor r (oder auch x) eingeführt werden, der von einem willkürlich gewählten Ursprung (meist dem Startpunkt) zur momentanen Position gerichtet ist.

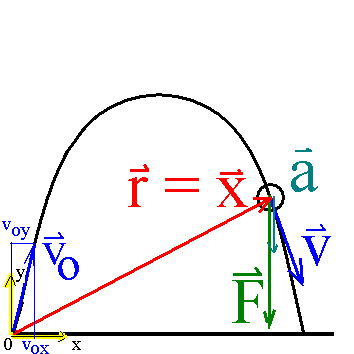Unterschiedliche Arten von Würfen unterscheiden sich durch die Vektoren des Anfangsortes x0 und der Anfangsgeschwindigkeit v0. Sonst gelten obige Beziehungen, hier für einen willkürlichen Zeitpunkt eingezeichnet. In allen Fällen sieht man: Kraft- und Bewegungsrichtung sind beim Wurf i.A. nicht gleichgerichtet. Das ist m.E. eine der wichtigsten Erkenntnisse, die der Schüler aus diesem Kapitel mitnehmen sollte.

Es kann sinnvoll sein, mit Spaltenvektoren dieses ohnehin plausible Ergebnis ein einziges Mal auch formal zu zeigen.

Umgekehrt kann der vektorielle (koordinatenfreie) Ansatz nach Übersetzung in die Koordinatendarstellung der Spaltenvektoren Ausgangspunkt für den Ansatz bei Rechenaufgaben sein, z.B. für einen schiefen Wurf. Wiederum: Einsetzen in fertige "Formeln" ist m.E. in diesem Zusammenhang sinnlos. Stattdessen erscheint es sinnvoller, Abhängigkeiten zu diskutieren, z.B. "Wie groß ist die Wurfweite bei doppelter, dreifacher, ... Startgeschwindigkeit, wie bei doppelter, dreifacher, ... Abschusshöhe?".

Motivation zu Vorhersagen und theoretischen Herleitungen lassen sich mit einem Schülerversuch (SV) gewinnen:

	Mit SV-Bauteilen wird eine schiefe Ebene aufgebaut (halbe Regalbretter oder Alu-U-Schienen); 10 cm der Tischplatte dienen als "Schanzentisch"; Glättung der Kante mit Klebestreifen. Man lässt eine Stahlkugel herunter rollen und misst die Wurfweite, z.B. durch Eindrücke auf einer Styropor- Platte auf dem Boden. Bei fester Bahnneigung wird die Anfangsgeschwindigkeit eingestellt durch unterschiedliche Starthöhen H. Dabei erscheint es sinnvoller, statt absoluter Werte der Anfangsgeschwindigkeit zu bestimmen, Verhältnisse zu diskutieren (doppelte, vierfache, ... Starthöhe: auch doppelte, vierfache, ... Anfangsgeschwindigkeit?).
	Der Wurfweite-Anfangsgeschwindigkeits-Graph (eine recht gute Ursprungsgerade) fordert zu theoretischen Überlegungen heraus.

III Vektorielle Verallgemeinerung der Newtonschen Mechanik

Dabei geht es mehr um eine koordinatenfreie Schreibweise von Vektoren mit der Betonung von Richtung und Betrag. Die vorherigen Überlegungen sind kompatibel mit der Folgerung aus der formalen Rechnung, insbesondere mit der allgemeinen Aussage, dass Kraft F und Beschleunigung a immer gleichgerichtet sind:

Ganz entsprechend werden auch die Grundgleichungen der eindimensionalen Kinematik vektoriell verallgemeinert.

Das ist Anlass, um noch einmal ausdrücklich zu formulieren:

IV Entsprechend des Kausalitätsprogramms der  Newtonschen Mechanik lassen sich bei bekannten Anfangsbedingungen und bei bekannter Kraft alle Würfe in ihrem Zeitverlauf vorhersagen:

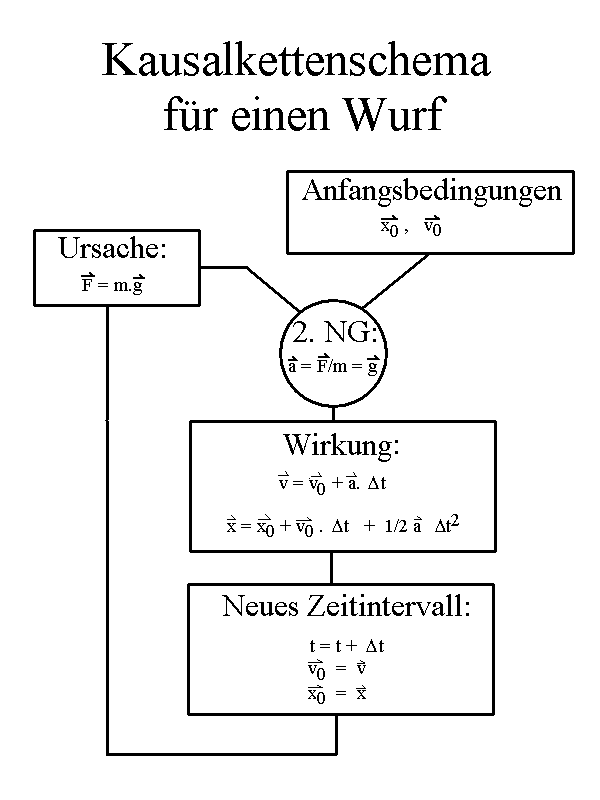Nach diesem Schema (formuliert entsprechend der "Methode der kleinen Schritte") kann jeder beliebige Wurf ohne Luftreibung durchgerechnet werden. Bei leichter Abänderung für F lässt sich auch Luftreibung erfassen. Für den konkreten Fall (horizontaler, schiefer... Wurf) müssen die Anfangsbedingungen genauer festgelegt werden. Dazu sind eventuell die Vektorgleichungen des Schemas in Koordinatengleichungen zu übersetzen. Das Schema könnte die Grundlage von Rechnungen auf dem Papier oder von Simulationen mit dem PC (z.B. mit einem Tabellenkalkulationsprogramm) mit und ohne Luftreibung sein.