© Horst Hübel Würzburg
2005 - 2014
Harmonische Schwingungen
|
Wesentliche Aspekte hier sind die wirkenden Kräfte, insbesondere eine rücktreibende Kraft nach dem Hookeschen Gesetz (F = - D·x), und in der Kinematik das Zusammenspiel von x, v und a. Nebenbei fällt aus dem Kraftgesetz und dem 2. NG eine Beziehung für die Schwingungsdauer an. Die Unabhängigkeit der Schwingungsdauer von der Amplitude kann als eine der definierenden Eigenschaften der harmonischen Schwingung aufgefasst werden.
Die Schüler wollen immer gleich zu Anfang die Gewichtskraft ins Spiel bringen. Ihr Vorschlag wird bestätigt: Ja, die Gewichtskraft ist dafür zuständig, dass sich eine neue Ruhelage ergibt. Betrachtet man aber die Bewegung um die neue Ruhelage - der Koordinatenursprung wird in die neue Ruhelage gelegt - , kann man die Gewichtskraft völlig vernachlässigen (wie später auch gezeigt werden kann). Ein horizontal aufgebautes Pendel auf der Luftkissenfahrbahn mit zwei waagrechten weichen Federn zeigt ebenfalls, dass die Gewichtskraft auf den Zeitverlauf keinen Einfluss hat. Ich halte es für verfehlt, die Erarbeitung der Gesetzmäßigkeiten hier mit einer Koordinatentransformation zum Nachweis dieser Überlegungen zu beginnen. So wichtig ist der Gesichtspunkt nicht, und wenn die harmonische Schwingung verstanden ist, lässt er sich relativ leicht nachtragen. Andernfalls besteht die Gefahr, dass ein Verständnis der eigentlichen Schwingung blockiert wird.
Besonders geeignet zur Untersuchung von harmonischen Schwingungen eines hängenden oder horizontalen Federpendels erscheinen Untersuchungen mit berührungslosen Bewegungsmesswandlern wie dem Sonarmeter oder dem IR-Bewegungssensor zusammen mit einem geeigneten PC-Programm, z.B. SONAR. Der IR-Bewegungssensor bei einer Reichweite von 10 - 80 cm ist besonders für Schülerversuche geeignet (Vgl. Buch Schülerversuche mit PC und ... ). Abgesehen von der eingeschränkten Reichweite erhält man ähnlich überzeugende Ergebnisse wie mit dem Sonarmeter.
 |
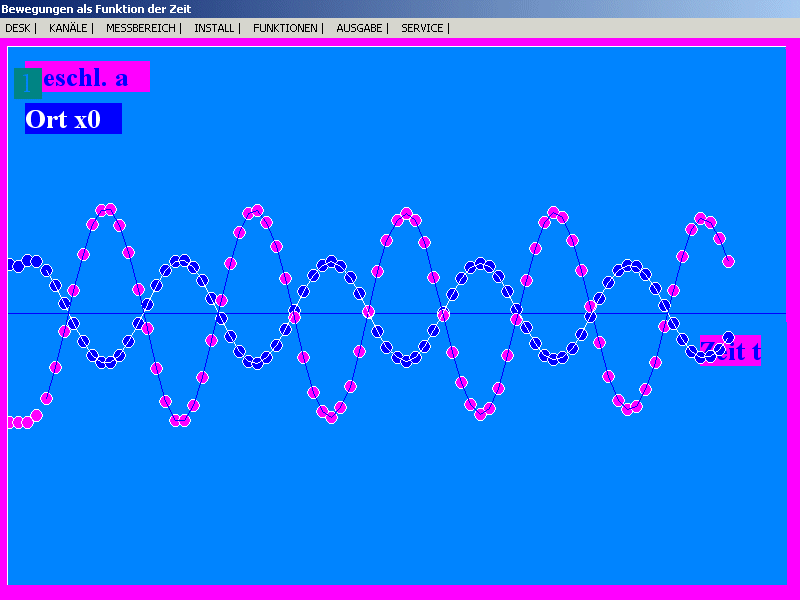| Registrierung einer harmonischen Schwingung mit einem Sonarmeter und
dem PC-Programm SONAR.
Gezeigt sind Auslenkung x (Ort) und Beschleunigung a in Abhängigkeit von der Zeit t. Die perfekte Gegenphasigkeit ist deutlich erkennbar. |
 |
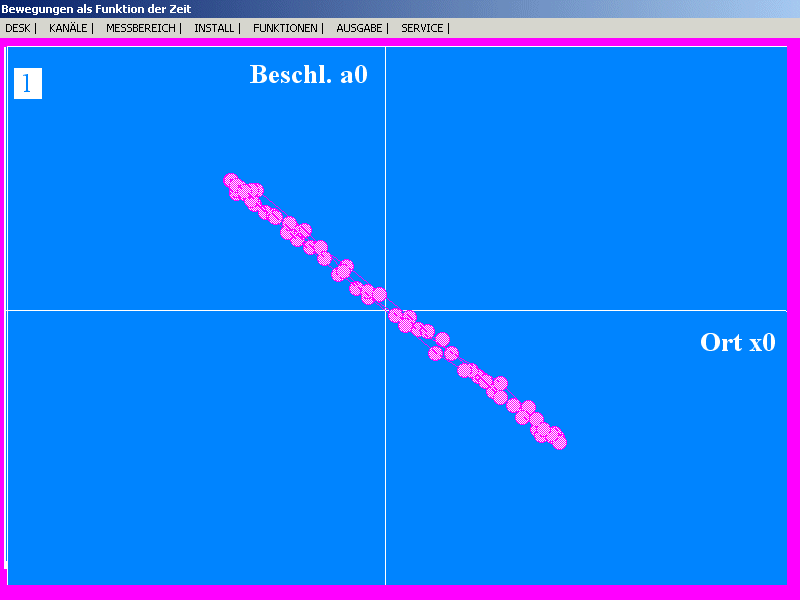| Registrierung einer harmonischen Schwingung mit einem Sonarmeter und
dem PC-Programm SONAR: a-x-Darstellung (Kraftgesetz).
Einerseits ist wie im vorigen Diagramm die perfekte Gegenphasigkeit von x und a erkennbar, anderseits auch die direkte Proportionalität: Nachweis des besonderen Kraftgesetzes der harmonischen Schwingung: F = -D.x, des Hookeschen Gesetzes. |
 |
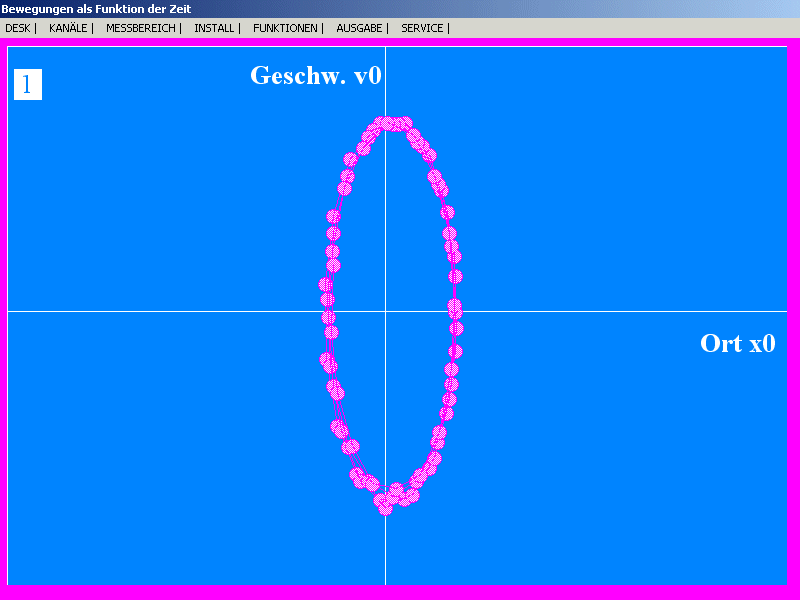| Registrierung einer harmonischen Schwingung mit einem Sonarmeter und
dem PC-Programm SONAR: x-v-Darstellung (Phasendiagramm).
Aus der Lage der Ellipse könnte man auf die 900-Phasenverschiebung zwischen x und v schließen. Das Diagramm ist aber auch Ausdruck des Energie-Erhaltungssatzes: Bei geeigneter Skalierung entsteht ein Kreis, dessen konstanter Radius x2 + a v2 mit dem Skalierungsfaktor a proportional zur konstanten Gesamtenergie D/2( x2 + w2 v2 ) ist. |
 |
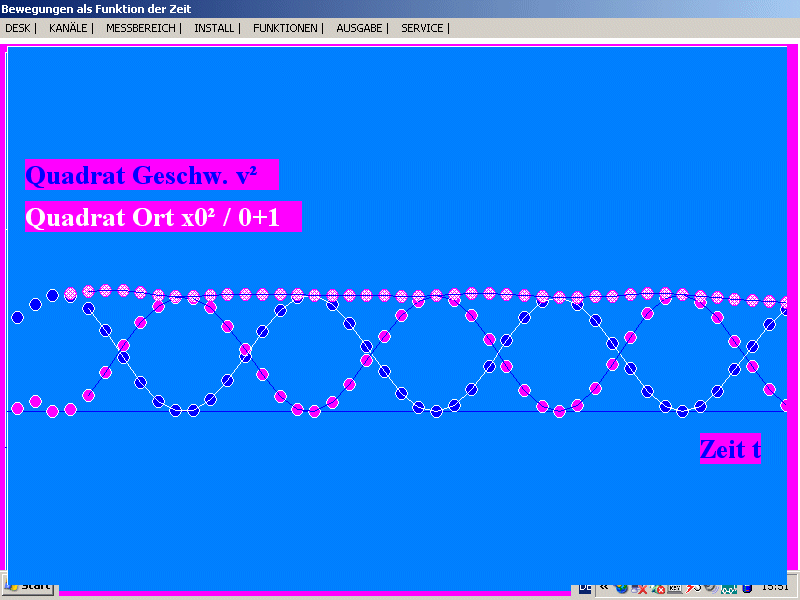| Registrierung einer harmonischen Schwingung mit einem Sonarmeter und
dem PC-Programm SONAR:
Darstellung von x2 und v2, geeignet mit Hilfe der Maus skaliert, und ihrer Summe. Diese ist ein Maß für die Gesamtenergie. Die Energieerhaltung kommt klar heraus. Wichtig ist, dass das Sonarmeter zunächst möglichst exakt die Ruhelage des Federpendels ermittelt. Dazu besitzt das Programm SONAR eine eigene, bequem handhabbare Funktion. |
Wenn die Schülern das abwechselnde Auftreten von potentieller und kinetischer Energie entsprechend dieser Graphik erarbeitet und verstanden haben, ist es sinnvoll, den Energieerhaltungssatz auch formal herzuleiten. Dabei wird der Zusammenhang zwischen Federkonstante D, Masse m und Kreisfrequenz w bzw. Schwingungsdauer T benötigt bzw. gewonnen.
.
.